薄壁不锈钢管超声波探伤中的信号处理技术方法

 汽车发动机中薄壁不锈钢管以奥氏体不锈钢为主，奥氏体不锈钢的超声波探伤历来是行业内重点研究内容。因为奥氏体组织本身晶粒度较大，会产生大量的干扰信号，给时域内超声缺陷信号判断带来极大困难。本书将以短时傅里叶变换信号处理技术为基础，简要介绍奥氏体不锈钢无缝钢管裂纹缺陷的信号处理方法。

一、短时傅里叶变换

短时傅里叶变换的实质是一种加窗后的移动傅里叶变换，假设有一信号s(t),其短时傅里叶变换的定义如下：

 根据式（4.9)~式（4.11),在某特定时刻b,用宽度为2τ的时间窗截取信号s(t),对所得信号做快速傅里叶变换，可获得信号s(t)在特定时刻b的幅度谱，将时间窗后移，依次进行相同操作，最终得到某一频率的信号在整个信号有效时间内的幅度谱，该方法称为短时傅里叶变换。

 1. 窗函数类型选择

 对短时傅里叶变换而言，窗函数与窗函数宽度的选择是关键因素，不同的窗函数有各自的频率特性，窗宽度的选择要同时考虑时间分辨率和频率分辨率。

  图4.13为304奥氏体不锈钢无缝管粗晶反射信号，反射信号长度为46个采样点，按窗宽度50个采样点选择不同窗函数分别做STFT处理。不同窗函数的STFT处理结果如图4.14所示。

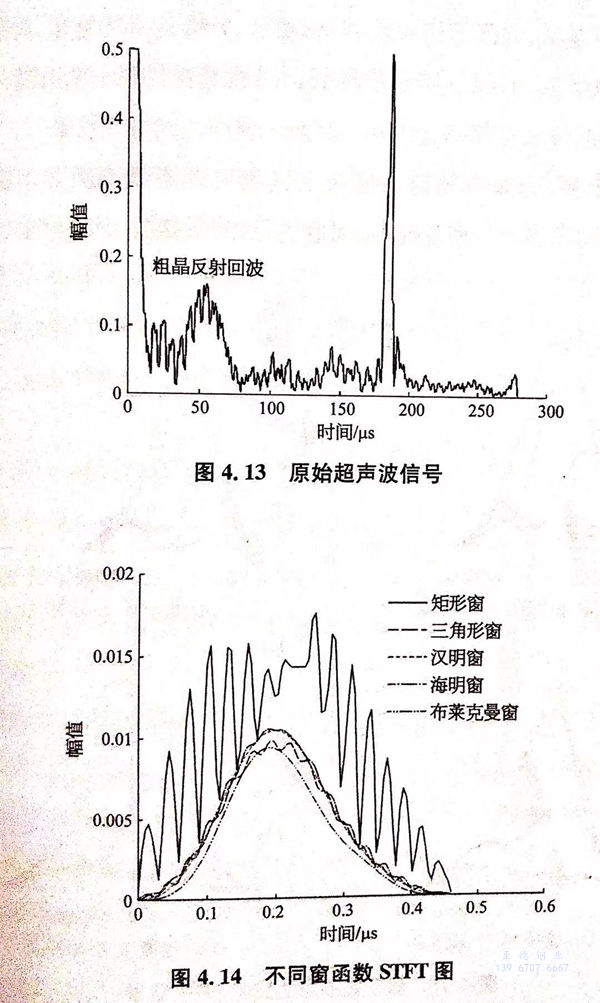
 分析不同窗函数STFT图，矩形窗、三角形窗以及海明窗STFT处理后的信号粗糙，光顺度不够，信号峰值较难获取，不宜采用；汉宁窗以及布莱克曼窗STFT处理后的信号比较顺滑，信号峰值较易确定。对比汉宁窗、布莱克曼窗，汉宁窗STFT处理所得信号幅值较大，分辨精度较高，故选择该窗函数较为适宜。

2. 窗函数宽度选择

 分析窗宽度是短时傅里叶变换的一个重要参数，窗宽度的选择决定能否正确分析出原始信号中的频率变化情况。分析窗宽度越窄，局部频谱的频率分辨率就越低，时间分辨率就越高；相反，分析窗宽度越宽，局部频谱的频率分辨率就越高，时间分辨率就越低。因此需要找到一个合适的分析窗宽度，使得局部频谱在频率分辨率与时间分辨率达到最优效果。

 采用汉宁窗，选择不同窗宽度对上述奥氏体不锈钢粗晶反射信号做STFT处理，得到多个频率的时间－幅值谱，其结果如图4.15所示。

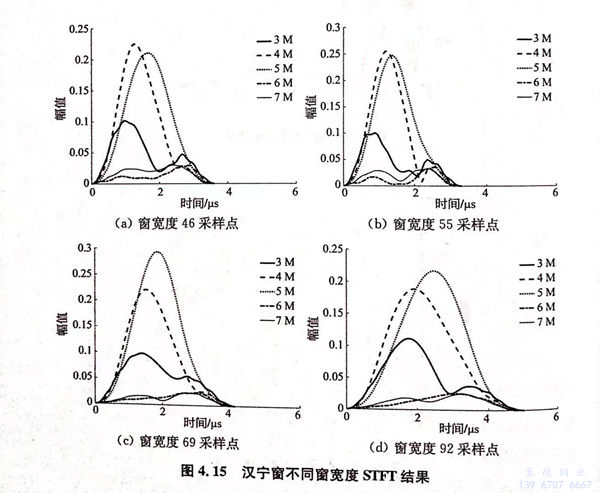
 分析图4.15a,当窗宽度等于超声反射信号长度时，处理结果的频率分辨率不足，其中4MHz、5MHz单频信号较难分辨；图4.15b窗宽度增加到反射信号长度的1.2倍，单频信号的频率分辨率有所增加；图4.15c窗宽度为反射信号长度的1.5倍，单频信号的时间分辨率及频率分辨率均达到最优；图4.15d窗宽度等于反射信号长度的2倍，单频信号的时间分辨率明显降低。因此STFT处理的窗函数最佳宽度应在超声反射信号长度的1.5倍左右。

二、粗晶奥氏体不锈钢管裂纹缺陷检测

 以外径21mm、厚度3.2mm的304奥氏体不锈钢无缝钢管为基管，细晶试样不做热处理，通过1280℃/4h的热处理工艺获得粗晶试样，分别在细晶和粗晶样管上通过电火花加工人工缺陷长5mm、深0.2mm、宽0.2mm,检测超声中心频率5MHz,超声检测信号如图4.16所示。

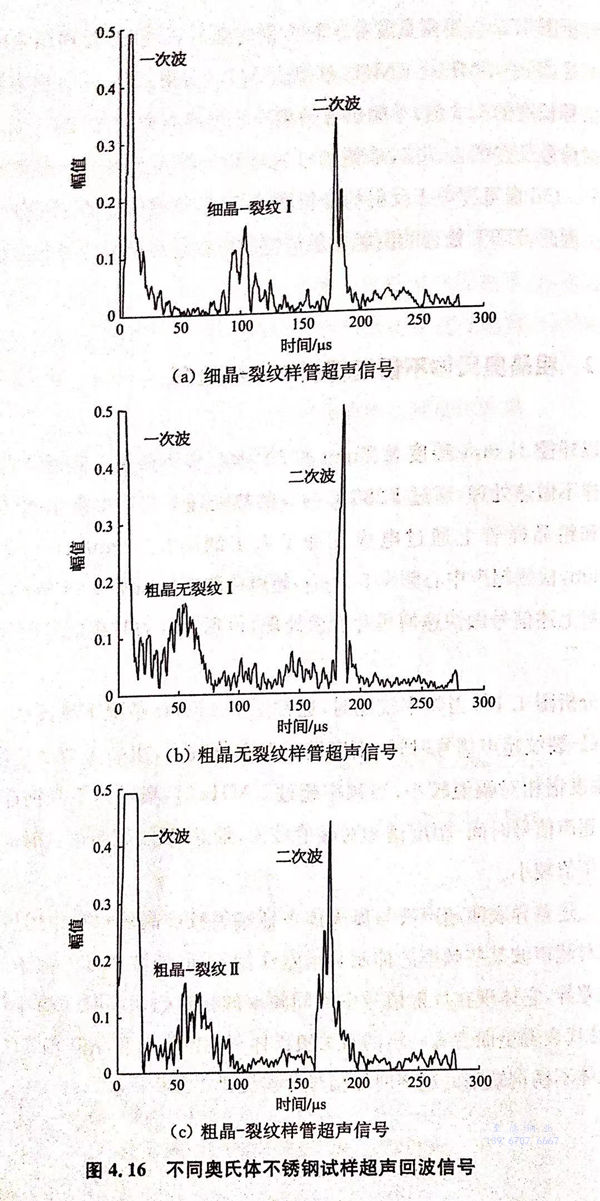
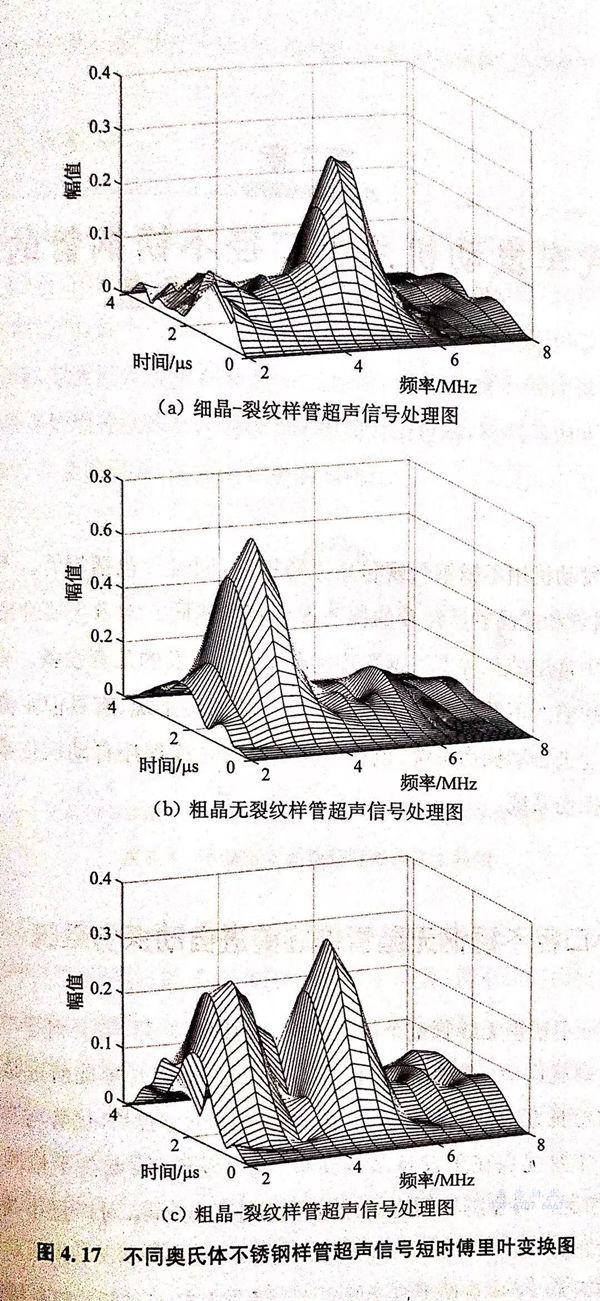
 对上述信号做快速傅里叶变换处理，得到各自的时频信号图如图4.17所示。

 分析图4.17,当频率较低时，通常低于4MHz情况下奥氏体不锈钢样管细晶－裂纹超声信号时间－幅度谱相对幅值较大，粗晶无裂纹超声信号时间－幅度谱相对幅值较小；当频率超过5MHz时，奥氏体不锈钢样管粗晶－裂纹超声信号时间－幅度谱相对幅值较大，细晶－裂纹超声信号时间－幅度谱相对幅值较小。

上述差异表明超声波与奥氏体不锈钢裂纹或晶粒相互作用后，裂纹和晶粒对超声波某些频率的抑制和增强作用不同，回波信号的频率成分会表现出差异，它体现在反射信号中不同频率的相对幅值随时间的变化规律不同，这代表着里面含有一定的有关奥氏体不锈钢裂纹和晶粒的信息，对粗晶奥氏体不锈钢缺陷的超声时域信号分辨提供了分析手段。